初めてのJijModeling: Getting started

この記事ではJijModelingを初めて使う方向けにJijModelingを使って数理モデリングを行う方法を紹介します。

JijModelingでは数理モデリングを行う際に、データが入るところをPlaceholderという変数で記述して、最初にデータに依らない形で数理モデルを構築します。その後にPlaceholderにデータを流し込んで数理モデルを完成させます。

早速簡単な問題でJijModelingを始めてみましょう。

JijModeling を使った数理モデリング

まず簡単な以下の数理モデルをJijModelingを使ってモデリングしてみましょう。

$$\begin{aligned} \min &\sum_{i=0}^{n-1}d_ix_i\\ \mathrm{s.t.}&\sum_{i=0}^{n-1} x_i = 1\\ &x_i \in \{0, 1\}, ~\forall i \end{aligned}$$

単純に1番小さい$`d_i`$を探す問題です。

JijModelingでは以下の順番でモデリングをおこないます。

1. データを入れる変数をPlaceholderを使って定義する.
2. 最適化したい決定変数を定義する.
3. Problemクラスのインスタンスを作成する.
4. problemに目的関数 (最小化したい関数) を追加する.
5. problemに制約条件を追加する.
6. Placeholderに流し込むデータを用意する.
7. problemにデータを流し込んで, 使うソルバー向けに変換する.
8. ソルバーで解く.

1~5までのステップがJijModelingを使った数理モデリングとなります。では早速JijModelingを使っていきましょう。

1. データを入れる変数をPlaceholderを使って定義する

まずデータ（インスタンス）となる$`d_i`$という変数を定義します。

import jijmodeling as jm

d = jm.Placeholder("d", dim=1)
n = d.shape[0]

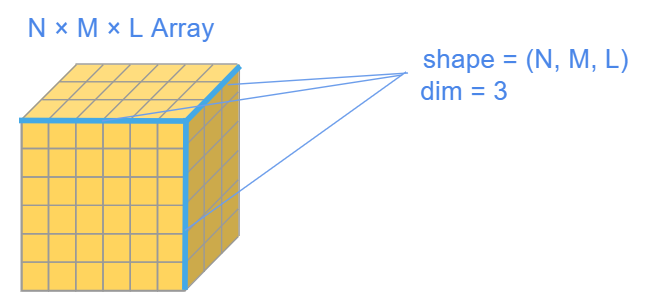
ここでPlaceholderの引数のdimは変数dに代入する値が1次元配列である、つまりdの添字は一つであるということを意味しています。そしてn = d.shape[0]はdの長さを取得しています。

dim, shapeのイメージは以下の画像を参考にしてください。

2. 最適化したい決定変数を定義する

次にこの問題の決定変数であるxを定義します。 長さnの一次元配列の0-1変数を定義しましょう。

x = jm.Binary("x", shape=(n, ))

0-1変数はBinaryを使って表します。決定変数はdimではなく、shapeを用いてその配列の形を決定します。ちなみにPlaceholderの大きさもshapeで指定することは可能です。

3. Problemクラスのインスタンスを作成する

problem = jm.Problem("sample")

適当な名前をつけてProblemインスタンスを作成します。Problemインスタンスに目的関数や制約条件を追加していきます。

4. problemに目的関数 (最小化したい関数) を追加する

ここでの目的関数は

$$\min \sum_{i=0}^{n-1}d_ix_i$$

でしたので、こちらをJijModelingを使ってモデリングします。

i = jm.Element("i", (0, n))

problem += jm.Sum(i, d[i]*x[i])

ここでiが総和で用いてる添字で(0, n)はiが0からn-1まで動くことを表しています。Pythonのrangeと同じようにnが含まれない（つまりn-1まで）となることに注意してください。

またSum関数は第一引数に総和で用いるElementオブジェクトを、第二引数には総和を取る数式を記述します。詳しくは 2. 総和演算 Sum の記事を参照してください。

!!! note "d[i]の[]について" 変数オブジェクトに対しての[]演算子ですが、実際は配列のようにi番目の要素を取り出しているのではなく、d変数に添字iを追加している操作です。

5. problem に制約条件を追加する

制約条件は

$$\mathrm{s.t.} \sum_{i=0}^{n-1} x_i = 1$$

でした。こちらをモデリングしていきます。

problem += jm.Constraint("onehot", x[:] == 1)

制約条件はConsraintを使って記述します。第一引数には制約条件につける名前を第二引数には条件を記述します。また係数が特にない変数に対する単純な総和は:を使うことで簡単に記述することができます。つまりx[:]はjm.Sum(i, x[i])と同じ意味です。

制約条件については 3. 制約条件 Constraint を参照してください。

ここまでのまとめ

ここまでの実装をまとめます。

import jijmodeling as jm

d = jm.Placeholder("d", dim=1)
n = d.shape[0]

x = jm.Binary("x", shape=(n, ))

problem = jm.Problem("sample")

i = jm.Element("i", (0, n))

problem += jm.Sum(i, d[i]*x[i])
problem += jm.Constraint("onehot", x[:] == 1)

まとめてみると非常にシンプルに記述できています。

このように数式を書くのと同じように直感的に書けるのがJijModelingの特徴です。さらに直感的に書くためにモデリングしたproblemを数式の形に出力してちゃんと実装できているかの確認を行うことができます。この記事の最後のセクションを参照してください。

ここまでの記述ではdの具体的な値は決まっていません。ここから具体的なdの値をセットして使いたいソルバー向けに数理モデルを変換する処理をおこないます。

JijZeptまたはOpenJijを使って問題を解く

ここではJijZeptまたはOpenJijを使って解く二通りの解き方を紹介します。

JijZeptで問題を解く

JijZeptを契約している方はJijModelingでモデリングした数理モデルと流し込むデータを渡すことで問題を解くことができます。

import jijzept as jz


data = {"d": [1, 2, -1, -3, -1]}

sampler = jz.JijSASampler()
response = sampler.sample_model(problem, data, {'onehot': 4})

JijZeptでは各Samplerクラスの.sample_modelを使って解きたい問題を送信することができます。詳しくはJijZeptのドキュメントを参照してください。

ローカルでPyQUBOに変換してOpenJijを使って解く

手元でJijModelingでモデリングした結果を調べたい場合は、PyQUBOに変換することでOpenJijなどのソルバーに投げることができます。

import openjij as oj

data = {"d": [1, 2, -1, -3, -1]}

# PyQUBOへの変換
pyq_obj = problem.to_pyqubo(data, {})

# ここからはPyQUBOの機能を使ってOpenJij向けに変換
bqm = pyq_obj.compile().to_bqm(feed_dict={'onehot': 4})

sampler = oj.SASampler()
response = sampler.sample(bqm)

問題をデコードして見やすくする

JijZept, OpenJijの両方ともにresponseという結果を得ました。しかしながらこのresponseは解を確認するのには少し見にくいのでJijModelingのデコード機能を使って解を見やすくし、制約条件が満たされているかのチェックなどをおこないます。

# 解をデコード & 制約条件のチェックを行う
decoded = problem.decode(response, data, {})
print(decoded.solutions)
print(decoded.objectives)
print(decoded.constraint_expr_value)
print(decoded.constraint_violations)

デコードされた結果をみると決定変数 x が numpy.ndarray に変換されて出力されていることが確認できます。

ここまでがJijModelingの基本的な流れです。より複雑な制約条件を用いたい場合などは他の記事を参照してください。

Jupyter notebook を使って数式の作成と実装を確認しながら行う

JijModelingをJupyter notebookを使うと数理モデルがどのような数式になっているかを確認しながら実装していくことが可能です。

例えば以下の画像のように数式を確認しながら実装を行います。

数理モデルを実装する際の問題点の一つとして実装して出てきた解が変な解の場合、実装が悪いのか元の数理モデルが悪いのかがパッと見ても分からない場合があります。

JijModelingでは実装が数式だとどのように見えるかを可視化できるので実装と考えている数式がちゃんと対応しているかを即座に確認することができます。

ぜひJupyter notebookを使ってこちらの機能を試してみてください。

!!! info "Google colaboratory の 場合" Google colaboratory では上記の数式で出力する機能が使えないことが確認されています。そのため数式で出力しながら実装する機能はローカルのJupyter notebook環境を利用してください。